🧠 大模型中的“权重”概念
在大模型(LLM)的语境下,权重是指模型中的参数(Parameters),它们是模型在训练过程中学习到的数值。
简单来说,如果把大模型想象成一个巨型的人脑网络,那么:
- 神经元(Neurons):是信息处理的基本单位。
- 连接(Connections):是神经元之间传递信息的路径。
- 权重(Weights):就是这些连接上的“强度”或“重要性”数值。
1. 权重的本质和作用
- 数值集合(The Numbers):权重是模型中数十亿甚至数万亿个**浮点数(Floating-point numbers)**的集合。
- 知识和规则(Knowledge & Rules):这些数值共同编码了模型从海量训练数据中学到的语言结构、语法规则、世界知识、事实信息以及推理能力。
- 计算的核心(The Core Calculation):在模型进行推理(如生成一个回复)时,输入数据(文本、图像等)会在每一层神经网络中与这些权重进行矩阵乘法等运算。权重决定了输入信息应该如何被组合、转换和传递到下一层。
例如: 当模型看到“猫”这个词时,与“猫”相关的权重可能被激活,并指导模型在生成下一个词时偏向于“抓”、“毛茸茸”、“宠物”等词汇。
2. 权重和模型大小的关系
- 参数量(Parameter Count):通常用来衡量一个模型的大小。一个 $8\text{B}$ 模型就有 80 亿个参数(即 80 亿个权重值)。参数量越大,理论上模型能编码的知识和处理复杂任务的能力就越强。
3. 权重分布和量化的关系(承接 INT4 话题)
当讨论到**量化(Quantization)**时,权重分布变得非常重要:
- 分布特点(Distribution):大型模型的权重值通常呈窄而高的正态分布(Normal Distribution),这意味着绝大多数权重的值都集中在 0 附近。
- 量化优化(Optimization):INT4 量化技术(如 NF4)正是利用了这一特点。
- NF4 (Normalized Float 4) 是一种针对正态分布权重优化的数据类型,它能更有效地将这些集中在 0 附近的浮点值映射到 4 位的整数空间,从而在大幅压缩存储空间的同时,最大限度地减少信息损失。
因此,“权重”是模型的大脑和记忆,而“权重分布”是它的数值特征,决定了我们能用多高效的方式(如 INT4 量化)来存储和运行它。
1. 正态分布的特点与量化挑战
大型语言模型的权重(Weight)在训练后,通常表现为**以零为中心的、服从正态分布(Normal Distribution)**的形状,也被称为“钟形曲线”:
- 特点一:高度集中于中心 (0)。
- 含义: 绝大多数的权重值都非常接近 $0$(例如,在 $-0.1$ 到 $+0.1$ 之间)。这些“小值”贡献了模型的绝大部分信息和功能。
- 量化挑战: 如果采用均匀量化(即,将数值范围平均分配给 $2^4 = 16$ 个量化点),那么大部分量化点会被浪费在极值(如 $-1$ 或 $+1$)上,而权重集中的 $0$ 附近只有很少的量化点。这会导致 $0$ 附近的细微差别被粗略地映射到相同的量化点,造成严重的精度损失。
- 特点二:越靠近边缘,数值越稀疏。
- 含义: 只有极少数的权重值是较大的正数或负数(这些是模型中少数关键连接)。
- 量化挑战: 稀疏的极值(Outliers)虽然对模型影响大,但由于数量少,即使分配的量化点少一些,精度损失也可以接受。
2. NF4 如何匹配正态分布(非均匀量化)
NF4 的核心思想是实现非均匀量化,即在权重集中的区域分配更多的量化点,在稀疏的区域分配更少的量化点。
| 量化点 | NF4 的分配原则 | 均匀量化的分配原则 |
| 靠近 0 的区域 | 分配更多的量化点,使得 $0$ 附近的细微数值变化能被精确地编码。 | 数量少,数值间的间隔大。 |
| 远离 0 的区域 | 分配更少的量化点,允许数值间的间隔更大。 | 数量多,但大部分时候用不上。 |
NF4 实现这种匹配的关键在于它是一种归一化浮点格式 (Normalized Float 4):
① 步骤:归一化 (Normalization)
首先,NF4 会找到权重矩阵中的最大绝对值 $M$(即归一化常数),然后将所有权重值 $W$ 归一化到 $[-1, 1]$ 的范围内。
$$\text{W}_{\text{normalized}} = \frac{W}{M}$$
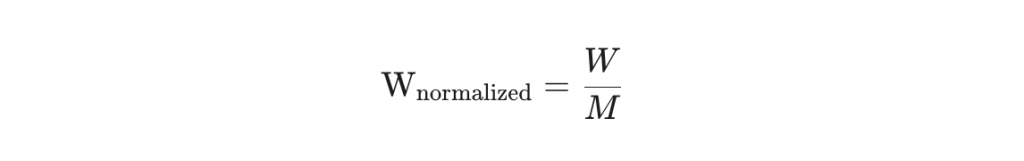
② 核心:信息理论最优 (Information Theoretically Optimal)
NF4 的设计是信息论最优的。这意味着在只有 4 位的约束下,它能够以最小的信息损失来编码正态分布的数据。
NF4 实际上定义了一个具有 $2^4=16$ 个离散值的码本 (Codebook),这些离散值的间隔是不等距的。这些量化点被巧妙地放置在归一化后的 $[-1, 1]$ 区间内:
- 量化点密集区: 大部分的量化点(如 10 个以上)被紧密地安排在靠近 $0$ 的区域。
- 量化点稀疏区: 只有少数几个量化点被用来表示远离 $0$ 的较大值。
这种非线性、非均匀的量化方式,确保了那些对模型性能贡献最大的小权重值(靠近 $0$ 的区域)能得到最高的编码精度,而对模型精度影响较小的极值则采用较粗略的编码,从而用最小的位宽(4 位)实现了最大的精度保留。
总结
NF4 能够与 LLM 的权重分布完美匹配,是因为它利用了正态分布**“中心密集,两端稀疏”的特性,通过非均匀分配**其 16 个量化点,将编码的精度资源集中在了最重要的“小权重”区域。这是实现高压缩率(4-bit)且低精度损失的关键所在。